(*Программа «Two-temperature Electrical
Resistivity in Solid Metal due to only Electron-Phonon Scattering» -
сокращенное название суть “Electron-Phonon 2T-sigma”*)
(*Вычисляет частоту столкновений s-электрона с импульсом p с фононами и затем
интегрированием по p коэффициент электропроводности*)
(*температура электронов TeK, ионов TiK*)
(*алюминий*)
TeK=900. ;
(*температура электронов в К*)
mu= -0.0000163852;
(*химпотенциал электронов в а.е. – атомные единицы, или единицы Хартри*)
TiK=900.
(*температура ионов в К*)
Ti=TiK/11605./27.2 ;
(*температура электронов в а.е.*)
Te=TeK/11605./27.2 ;
(*температура электронов в а.е.*)
rho=2.6989;
(*плотность
в г/см^3*)
A=26.982 ;
(*молярная масса *)
z=3.
(*заряд иона в а.е. z – число электронов в зоне проводимости в расчете на один атом *)
M=1836.*A ;
(*масса атома в а.е.*)
na= rho/A*6.022*0.148*0.1;
(*концентрация атомов в а.е.*)
re=M*na ;
(*плотность в атомных единицах*)
qD=(6*Pi*Pi*na)^(1./3)
(*квазиимпульс Дебая в атомных единицах*)
si=6.260 ;
(*скорость продольного звука в км/сек*)
vat=3.*(10^5)/137
;
(*а.е.
единица скорости*)
s1=si/vat
s=s1/5.1
(*скорость звука в атомных единицах*)
ens= -11.1/27.2;
(*ens - дно s-зоны в а.е.*)
mu0=0;
(*положение химпотенциала электронов при Te=0*)
m=((3.*z*na*Pi*Pi)^(2./3))/(2*(mu0-ens))
(*масса s-электрона в а.е.*)
(*вычисление константы томас-фермиевского экранирования
кулоновского взаимодействия за счет s-электронов. Это kap*)
Xx=100
te=(ens-mu)/Te ;
hs[tk_]=
Sqrt[tk]*Exp[te-tk]/((Exp[te]+Exp[-tk])^2);
UK=
NIntegrate[hs[tk],{tk,0.,Infinity}];
dnsdm=
Sqrt[2.]/(Pi*Pi)*((Sqrt[m*Te])^3)*UK/Te ;
kap=Sqrt[4*Pi*dnsdm]
(*обратная длина томас-фермиевского экранирования в а.е.*)
pF=Sqrt[2*m*(mu0-ens)]
(*Ферми-импульс в а.е.*)
en[p_]=ens+p*p/(2*m) ;
(*закон дисперсии электронов*)
(*вычисление частот столкновений электрона с импульсом p с
фононами*)
cnu=Pi/(re*s*s)*s*((4*Pi*z*na)^2)*2*Pi*m/((2*Pi)^3) ;
(*постоянный множитель для этих частот*)
w[q_]=cnu*q*q/((q*q+kap*kap)^2) ;
(*функция импульса фонона q, содержащая квадрат матричного элемента и множитель от фазового объема фонона*)
(*вычисляет случай 1 с испусканием фонона*)
p1=Sqrt[p*p] ;
(*импульс электрона после испускания фонона. Здесь пренебрегаем изменением абсолютной величины импульса электрона в результате испускания фонона.*)
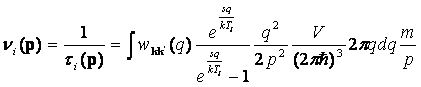
(*Выражение для частоты столкновений 
электрона с импульсом 
с фононами при их испускании (индекс i означает irradiation). Это выражение
представляет собой интеграл. Причем пределы интегрирования зависят от значения
импульса p электрона. Как эти пределы зависят от импульса, поясняется в
сопроводительном тексте «Пояснения к программе “Electron-Phonon 2T-sigma & kappa”».
Кроме того пояснения приведены ниже при описании рис. 1. В программе подынтегральная
функция в выражении для записывается в
следующем виде:*)
wp[p_,q_]=w[q]/p*(q*q-(p-p1)*(p-p1))/(2*p*p1)*Exp[s*q/Ti] /(Exp[s*q/Ti]-1) ;
(*Комбинация из нескольких постоянных сомножителей, входящая
в интеграл , была обозначена выше как «cnu» (constanta nu)*)
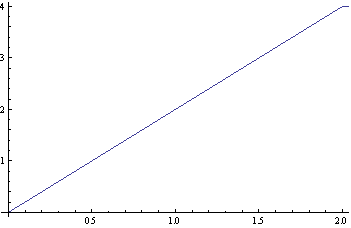
Рис. 1. На рисунке изображена область
интегрирования в интеграле в плоскости 
. Это плоскость электронного импульса 
и импульса фонона q. Метка 
на оси q на
рисунке соответствует дебаевскому импульсу. Метка 
– фермиевский импульс, где z – число электронов в зоне проводимости в
расчете на один атом. Прямая 
соответствует точному
рассеянию электрона назад. Квазиимпульс фононов ограничен значением 
. Поэтому область интегрирования ограничивают две прямые: и 
.
(* 0<p<0.5*qD *)
nup1[p_]= NIntegrate[wp[p,q],{q,0.0001, 2*p }] ;
(*В этой строке находится частота столкновений при
испускании фононов электрона с импульсом 0<p<0.5*qD.
См. рис. 1. Из-за излома на границе области интегрирования мы разбиваем
интеграл на два – один с 0<p<0.5*qD и другой с 0.5*qD <p<Infinity *)
(* 0.5*qD <p<Infinity *)
nup3[p_]= NIntegrate[wp[p,q],{q, 0.0001, qD}] ;
(*частота столкновений при испускании фононов электрона с импульсом 0.5*qD <p<Infinity *)
xx=123
(*вычисляет случай 2. Этот случай соответствует поглощению фонона*)
pm=Sqrt[p*p] ;
(*импульс электрона после поглощения фонона*)
wm[p_,q_]=w[q]/p*(q*q-(p-pm)*(p-pm))/(2*p*pm)/(Exp[s*q/Ti]-1) ;
(*подынтегральная функция для вычисления частот столкновения при поглощении фонона. Эта строка соответствует интегралу *)
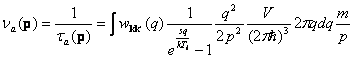
(* 0<p<0.5*qD *)
num2[p_]=
NIntegrate[wm[p,q],{q, 0.0001, 2*p }] ;
(*частота столкновений при поглощении фононов электрона с импульсом 0<p<0.5*qD *)
(* 0.5*qD <p<Infinity *)
num4[p_]= NIntegrate[wm[p,q],{q, 0.0001, qD}] ;
(*частота столкновений при поглощении фононов электрона с импульсом 0.5*qD<p<Infinity *)
(*вычисление коэффициента электропроводности*)
faw[p_] = 1./(( Exp[(en[p]-mu)/(2*Te)]+
Exp[-(en[p]-mu)/(2*Te)])^2)/Te*
p*p/m/m*2*2*Pi*p*p/((2*Pi)^3)*(2/3.);
(*faw - часть подынтегральной функции для вычисления коэффициента электропроводности. Коэффициент электропроводности представляет собой интеграл
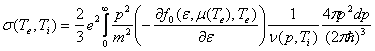
faw равно подынтегральному выражению без
множителя с частотой 
, где 
*)
iaw1 = NIntegrate[
faw[p] / (nup1[p] + num2[p]),{p, 0, 0.5*qD}]
(*Полный вклад в проводимость электронов с импульсами 0<p<0.5*qD *)
iaw2=NIntegrate[faw[p]/(nup3[p]+num4[p]),{p,
0.5*qD, 50. }]
(*Полный вклад в проводимость от электронов с импульсами 0.5*qD <p<Infinity*)
sigma = iaw1 + iaw2
(*Полная проводимость в а.е.*)
xxx=555
r = 0.148*9.1/(1.6*1.6*2.4)/sigma
(*это – удельное сопротивление в мкОм*м (система СИ) *)
nuat=z*na/(m*sigma) ;
(*это эффективная частота s-i столкновений в атомных единицах. Она вычисляется по формуле Друде*)
nus=nuat*41
(*это – частота в единицах 10^15 1/сек*)
xx=12345
nuF=nup3[pF]+num4[pF]
;
(*Полная частота столкновений с фононами электрона с импульсом Ферми:
. Она находится по приведенным выше формулам. При низких
электронных температурах 
электропроводность
определяется столкновениями на поверхности Ферми. При этом выражение для
проводимости
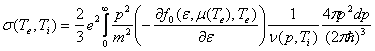
легко интегрируется, поскольку производная от функции Ферми
пропорциональна дельта-функции. Частота сначала подсчитывается
в а.е.*)
nuFa=nuF*41
(*частота столкновений с фононами электрона с импульсом Ферми в единицах 10^15 1/сек*)
rF=3./2*Pi*Pi*nuF/Sqrt[2*m*(mu0-ens)]/(mu0-ens)* 0.148*9.1/(1.6*1.6*2.4)
(*удельное сопротивление при частоте столкновений на уровне Ферми*)