Пояснения к программе “Electron-Phonon 2T-sigma”

(полное название программы:

Two-temperature Electrical Resistivity in Solid Metal

due to only Electron-Phonon Scattering)

 

Кинетическое уравнение для функции распределения  электронов в металле во внешнем электрическом поле напряженности при их столкновении с фононами выглядит следующим образом:

                                                         .

- импульс электрона, связанный с его волновым вектором соотношением .

Учитывая, что , получаем

                                                      .                                                              (1)

Установившаяся функция распределения электронов по импульсам во внешнем постоянном электрическом поле в приближении редких столкновений, когда сопротивление металла много меньше максимального металлического сопротивления, записывается в виде

                                                        ,

 - фермиевская функция, функция распределения электронов при отсутствии поля.- поправка, связанная с приложенным внешним электрическим полем и малая в меру малости поля. -химический потенциал электронов.

Правая часть уравнения (1) – столкновительный член. В приближении времени релаксации с энергией электрона  он записывается в виде .          

Учитывая малость и  , тогда кинетическое уравнение (1) записываем как

                                                                 .

Отсюда

.

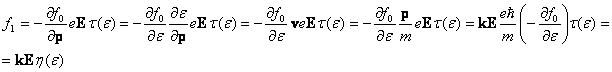                                                                                                                                                     (2)

 

Распишем теперь более подробно столкновительный член уравнения (1).

Число электронов, покидающих в единицу времени элемент фазового объема при испускании фонона (,- волновой импульс фонона,- волновой импульс электрона после испускания фонона), равно:

                         

(эффективная масса электронов, - скорость продольного звука). Множитель 2 здесь учитывает спиновое вырождение электронов.

 

- вероятность рассеяния электрона из состояния в состояние . При этом

                                                ,

(-плотность, -концентрация ионов, Z –заряд иона, -частота фонона).

 - Фурье-компонента экранированного кулоновского взаимодействия иона с электроном с длиной экранирования , где постоянная экранирования определяется в томас-фермиевском приближении как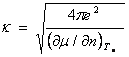

(-концентрация электронов). Тогда

                                               .

 

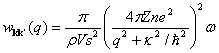 - бозевская функция, . Она дает распределение фононов. На этом распределении не сказывается наличие электрического поля и дрейфа электронов в этом поле.

Число электронов, покидающих в единицу времени элемент фазового объема при поглощении фонона (,- волновой импульс фонона,- волновой импульс электрона до поглощения фонона):

                         

Число электронов, входящих  в единицу времени в элемент фазового объема при испускании фонона (,- волновой импульс фонона,- волновой импульс электрона после испускания фонона):

                         

Число электронов, входящих в единицу времени в элемент фазового объема при поглощении фонона (,- волновой импульс фонона,- волновой импульс электрона до поглощения фонона):                     

                          .

Учитывая, что столкновения квазиупругие, , получаем

число электронов, покидающих в единицу времени элемент фазового объема при испускании фонона (,- волновой импульс фонона,- волновой импульс электрона после испускания фонона):

                          .

Число электронов, покидающих в единицу времени элемент фазового объема при поглощении фонона (,- волновой импульс фонона,- волновой импульс электрона до поглощения фонона):

                         

Число электронов, входящих  в единицу времени в элемент фазового объема при испускании фонона (,- волновой импульс фонона,- волновой импульс электрона после испускания фонона):

                         

Число электронов, входящих в единицу времени в элемент фазового объема при поглощении фонона (,- волновой импульс фонона,- волновой импульс электрона до поглощения фонона):                     

                          .

 

Изменение числа электронов в единицу времени в элементе фазового объема  за счет столкновения с фононами

 

                                      

                                        

                                        

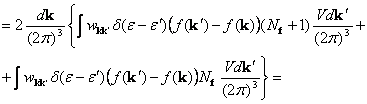
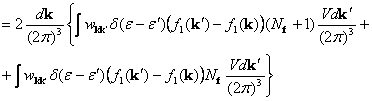
Подставляя сюда  в виде (2), получаем

                                         

                                        

                                        

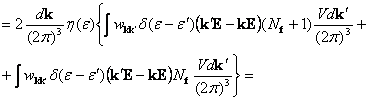
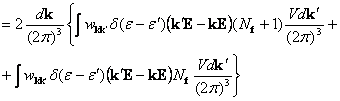
Учитывая , что при квазиупругих столкновениях ||=||= и вводя угол  между и, угол  между и, а также угол  между и и угол  между плоскостями,  и ,, получаем

                          (3)

 

При этом имеем

                                           ,

откуда

                              .                                 (4)

Если записать , то при интегрировании по  последнее слагаемое в (4) дает нуль, и из уравнения (3) получаем                            

Тогда

   ,

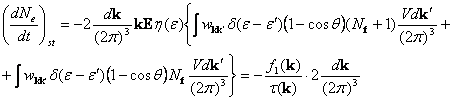где

   .          (5)

 

Учитывая, что - угол между векторами и  , равными по модулю , и , имеем

                                                              .

Интегрирование по при заданном заменяем интегрированием по (по . ). Обозначаем аргумент - функции

                              ,                                              (6)

где , а -угол между и . Тогда 

                                              .

Но из (6) получаем , поэтому

                                                  .

Введением переменной  выражение (5) для частоты столкновения с фононами электрона с волновым вектором может быть переписано в виде

   .

                                                                                                                                                   (7)

При  имеем , тогда из (6) следует, что интегрирование по   при  ведется в пределах от  до .

 

Учитывая, что и - модули векторов, нижний предел здесь всегда отрицательный (). Для того,  чтобы интегрирование дельта-функции  в выражении для  парциальной частоты столкновений (7) давало отличный от нуля результат, необходимо, чтобы верхний предел был положительным ().

 

Из условия  получаем . Учитывая еще, что (- дебаевский квазиимпульс, ), получаем область интегрирования в плоскости p-q:

 

                      

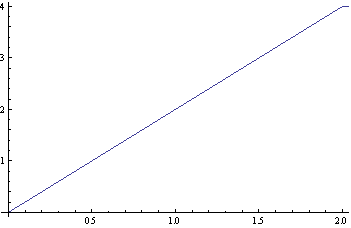                               p

 

Тогда при испускании фононов частота столкновений с ними электрона с импульсом

 ,

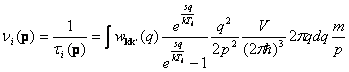и при поглощении фононов

 

 

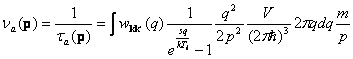
Согласно рисунку, интегрирование по  ведется от 0 до  при , и от 0 до при .

     По найденной полной частоте столкновений электрона с импульсом  с фононами как  при их испускании, так и при их поглощениипроводимость находится как

                         .

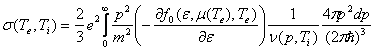Введем среднюю частоту электрон-фононных столкновений и условия, что подчиняется соотношению Друде-Лоренца

                                                     .

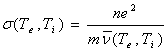Отсюда

                                                    .